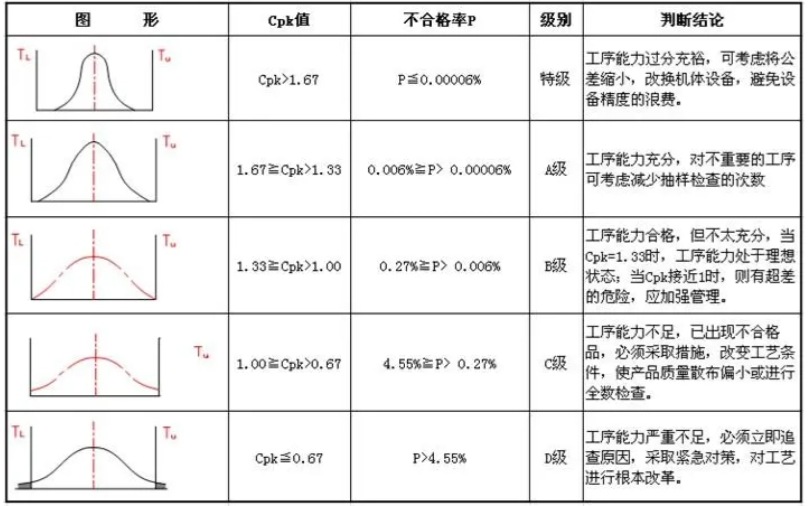
Cpk、Sigma和PPM的换算关系
过程能力指数（Cp和Cpk）其实就是衡量过程在稳定状态（即没有特殊原因干扰、生产过程处于可控状态）的情况下，产品能否满足质量要求的程度指标。
通常，Cpk值越高，表示产品的不良率越低，过程能力也就越强。
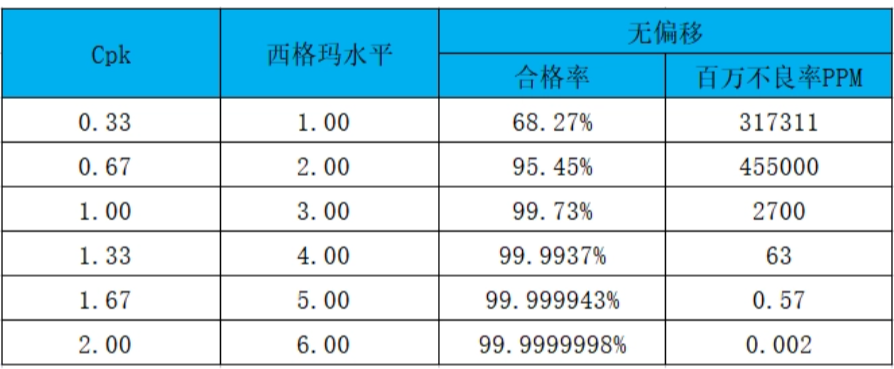
在PPAP审核中，SQE通常要求供应商提供的过程能力报告中，关键特性的Cpk需大于1.33，此时供应商内部的百万分之不良率（PPM）为63。
如果进一步分析Cpk=1.0和Cpk=1.67的情况，结果如下：
在没有考虑偏移的前提下：
Cpk=1.33对应4σ水平，其PPM为63.3；
Cpk=1.67对应5σ水平，其PPM为0.570；
Cpk=2.0对应6σ水平，其PPM为0.0020。
在过程能力指数Cp或Cpk稳定的前提下，可以利用正态分布公式将其转换为该产品或制程特性的良率或不良率，同时也可以进一步对应到西格玛水平。
Cp和Cpk反映的是过程能力，西格玛水平反映的是企业的管理水平，PPM则是管理结果的体现。
我们先从正态分布讲起：
正态分布(Normal distribution)
正态分布是最自然的分布，某一定范围内的所有实数值都可以取的概率分布，是计量型概率分布中最有代表性的分布。
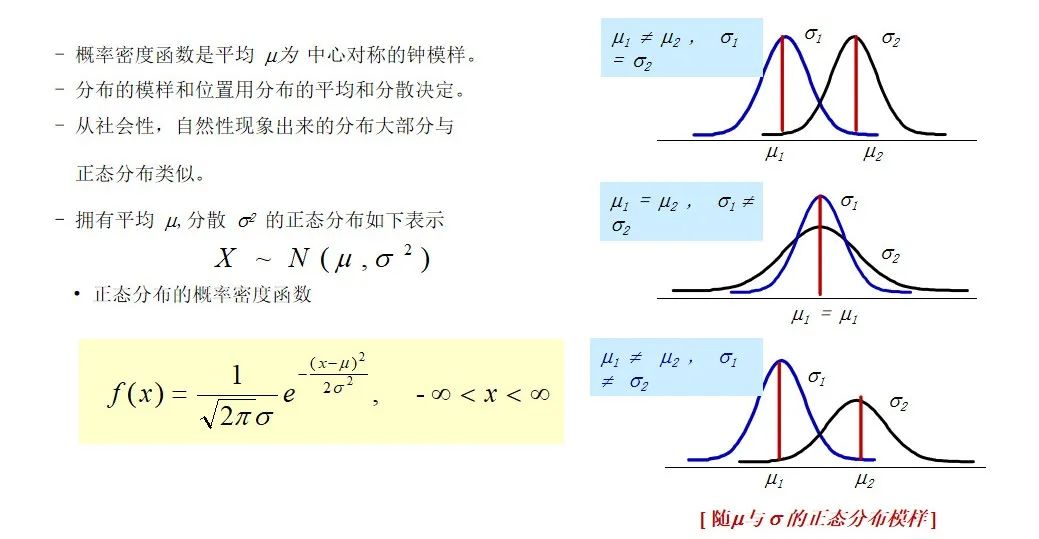
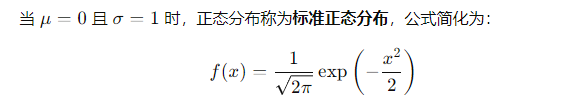
正态分布是过程能力分析的理论基础，通过其概率密度函数和积分性质，质量工程师能够计算产品特性在规格范围内的概率，从而评估过程能力和产品合格率。
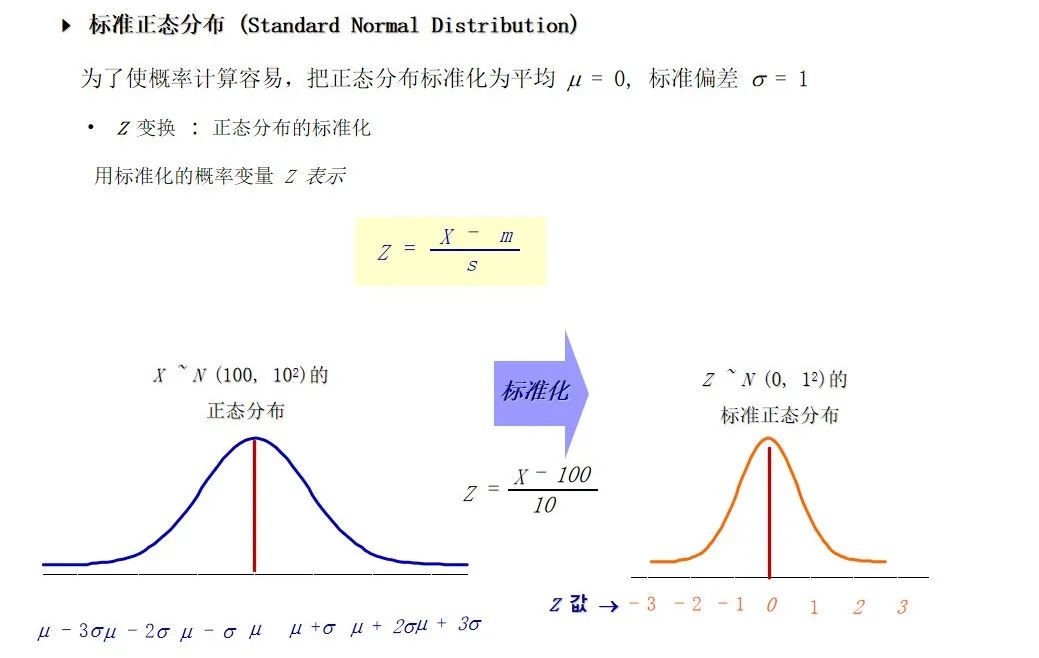
标准正态分布（μ=0,σ=1）是正态分布的一种特殊情况，便于简化计算和查表，为过程能力指数（Cp和Cpk）的计算提供了基础工具。
什么是西格玛水平？
西格玛水平是是一个用于衡量过程质量能力的指标，通常用于评估一个生产过程或业务流程满足质量要求的程度。
在质量管理中，西格玛水平越高，意味着产品的生产过程中，符合质量标准的合格品数量越多，缺陷的数量越少，反之，西格玛水平越低，缺陷的数量越多。
Cpk和西格玛水平之间的关系？
Cp是过程能力的一个度量，表示的是过程的变异范围是否能够被产品的规格限容纳。其计算公式如下：
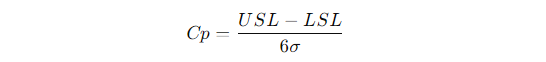
通过计算公式得出：
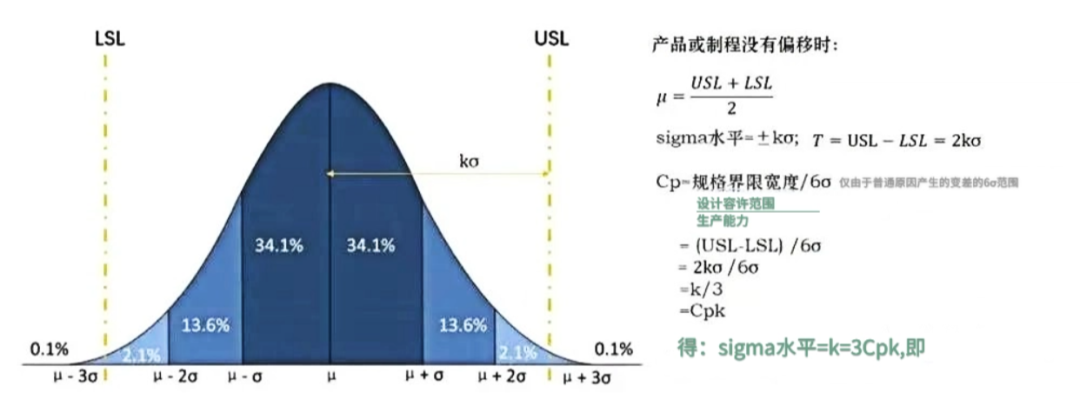
当Cpk=1.33时，西格玛水平=3*1.33（σ）=3.99（σ）≈4（σ），也就是说当Cpk=1.33时，即表示品质已经达到了4σ的能力。
接下来，我们讨论Cpk和PPM之间的关系。
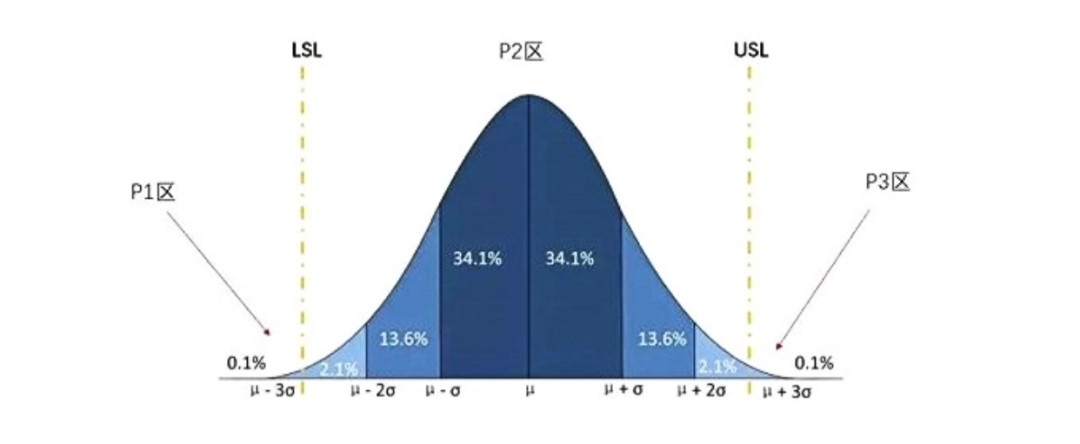
由下图，我们可知不良率为超过上规格线USL部分的面积，以及超过下规格线LSL部分的面积的总和。即：P=P1 + P3。
这里，我们引入正态分布的面积函数，标准正态分布函数F（x）。
该函数通过输入值x，可以得到相应的（-∞，x）的面积，即概率面积。
计算过后，我们得到了Cpk和不良率（PPM）的关系：
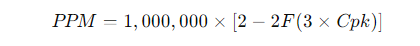
F(x) 表示标准正态分布的累积分布函数（CDF），即给定x值，F(x)返回正态分布小于x的概率。 Cpk 是过程能力指数，通常表示过程分布相对于规格限（USL和LSL）的能力。 3 × Cpk 是基于标准正态分布计算过程能力的转换，表示过程偏离目标的程度。
注：
1.在这个公式中，F(3 × Cpk) 是标准正态分布中，过程输出在3×Cpk倍标准差以内的累计概率。
2.因为PPM是指超过上规格限（USL）或下规格限（LSL）的缺陷产品数量，所以2 - 2F(3 × Cpk) 代表了超出规格限的概率，进而计算出每百万件产品中可能的不合格品数量。
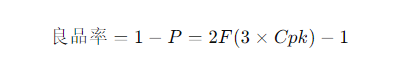
P 是不合格品的概率，等于超过上规格限（USL）或下规格限（LSL）的部分。 F(3 × Cpk) 是过程能力在3 × Cpk倍标准差以内的累积概率。 2F(3 × Cpk) - 1 则表示过程能力在目标范围内的合格产品比例。
注：
良品率（合格率）是1减去不合格品率。
根据标准正态分布，2F(3 × Cpk) - 1 可以算出产品在指定Cpk下的合格概率。
2.这个公式的本质是通过过程能力指数（Cpk）来判断，生产过程中有多少比例的产品会符合规格要求。
Cpk与均值偏移的影响
Cpk≠Cp
均值偏移时的不良率（PPM）计算
当过程均值发生1.5σ的偏移时，Cpk ≠ Cp，此时不良率的计算不再仅仅依赖于Cpk的直接公式。
为了反映这种偏移，我们通常通过在标准正态分布上加入一个1.5σ的偏移量来进行校正。
公式可以更新为：
此时，Cpk - 1.5 表示过程的实际能力考虑了均值偏移的影响。
